Calculating the Present and Future Value of an Annuity

Insurance companies calculate lifetime annuity payment schedules using complex actuarial tables. Single premium lifetime annuities can be purchased with a single lump sum. This period could be weekly, monthly, quarterly, annually or at any other regular time interval. Annuities that offer immediate payouts convert a one-time payment (sometimes known as a single premium annuity) into an ongoing payment stream. Payments last for a predetermined period of time, typically between five years and the buyer’s death. Immediate annuities best fit the needs of individuals close to retirement, with payments starting within the first year after one-time payment is completed.

• It can help you plan for the future by setting a particular goal for the future value and determining the amount and number of payments you’ll have to make to reach that goal.
• We are a team of finance, insurance, and actuarial professionals working to make it easier for everyone to achieve a steady and comfortable retirement.
• Say, for example, you’re given a choice between receiving a dollar today and waiting a year to receive it.
• An Ordinary Annuity is preferable when payments are more feasible at the end of a period, such as saving from a monthly salary.
• Usually the extra unknown variables are «unstated» variables that can reasonably be assumed.

Annuity Formula

• When interest growth is continuous, the payment schedule relies on a logarithmic scale.
• The higher the discount rate, the lower the present value of the annuity.
• You purchase the contract through either a lump sum payment or a series of payments and then receive monthly payments in retirement.
• Note that latexP/Y/latex and latexC/Y/latex are not main button keys in the latexTVM/latex row.
• Continuously compounding interest will cause annuities to generate slightly more value—although this also creates some calculation challenges.

Investors can determine the future value of their annuity by considering the annuity amount, projected rate of return, and number of periods. There are also implications as to whether the annuity payments are made at the beginning or at the end of a period. The future value of an annuity is the value of a group of recurring payments at a certain date in the future, assuming a particular rate of return, or a discount rate. As long as all of the variables surrounding the annuity are known, such as payment amount, projected rate, and number of periods, it is possible to calculate the future value of the annuity. Present value is an important concept for annuities because it allows individuals to compare the value of receiving a series of payments in the future to the value of receiving a lump-sum payment today. By calculating the present value of an annuity, individuals can determine whether it is more beneficial for them to receive a lump sum payment or to receive an annuity spread out over a number of years.

Determining the payment amount

The present value of an annuity allows you to accurately value the present worth of a series of annuity payments. You can use this information to come up with a cash equivalent for an annuity, which in turn helps you buy and sell annuities. This information can also help when comparing lump sum payments and future annuities. The payments are at the end of the payment intervals, and both the compounding frequency and the payment frequency are the same (both quarterly). Because this is a simple annuity, an interest rate conversion is not required.

Why Is Future Value (FV) Important to Investors?

If the contract specifies the period in advance, we call it a certain or guaranteed annuity. Therefore, the future value of your annuity due with $1,000 annual payments at a 5 percent interest rate for five years would be about $5,801.91. This slight difference in timing impacts the future value because earlier payments have more time to earn interest. Imagine investing $1,000 on Oct. 1 instead of Oct. 31 — it gains an extra month of interest growth. This concept helps you compare future income streams with current investment opportunities, allowing you to normal balance make informed financial decisions.

What Does Present Value Mean in the Annuity Formula?

• The future value factor is the aggregated growth that a lump sum or series of cash flow will entail.
• For simplicity, we refer to the ordinary annuity in the following specifications.
• Future value (FV) is the value of a current asset at a future date based on an assumed rate of growth.
• A lower discount rate results in a higher present value, while a higher discount rate results in a lower present value.
• In addition, you can use the STO and RCL buttons to store numbers and then recall them later.
• The account is expected to earn an average interest rate of 7% per year compounded quarterly.

Once you sign a contract with an insurance provider, you deposit a premium on which the insurance company pays interest regularly at a predetermined rate. After the contract completes, you receive both the principal and the accrued interest. You can also use the present Bookkeeping for Consultants value of an annuity due formula to calculate the present value of an annuity paid out or collected at the beginning of a predetermined time period. To calculate the future value of annuity due, make sure the calculator is in BGN mode. The easiest way to understand the difference between these types of annuities is to consider a simple example. Let’s assume that you deposit 100 dollars annually for three years, and the interest rate is 5 percent; thus, you have a $100, 3-year, 5% annuity.

The existence of a fiduciary duty does not prevent the rise of potential conflicts of interest. When Roberto’s son turns 18, the trust fund will have a balance of $63,672.39. If the winner was to invest all of his lottery prize money, he would have $2,544,543.22 after 25 years. After 11 years of $1,000 quarterly contributions, the client has $66,637.03 in the account.

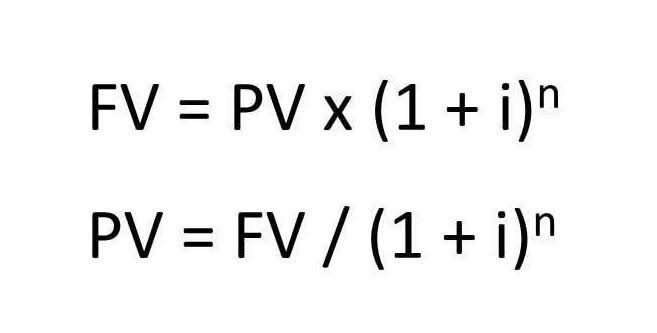
Method 1 – Using the FV Function to Get the Future Value of an Annuity

It’s essential to consider these implications in the overall financial planning process to optimize tax benefits and reduce liabilities. In terms of situational analysis, the choice between these two depends largely on the payment schedule and financial goals. An Ordinary Annuity is preferable when payments are more feasible at the end of a period, such as saving from a monthly salary. Annuity Due is more suitable when early payment is possible or desirable, such as in pension plans where early receipt is beneficial for covering immediate expenses. The additional (1+r) at the end of the formula accounts for the extra compounding period each payment receives.

RETIREMENT INCOME

Generally, the term is used to describe an investment product commonly sold by insurance companies and other financial service providers. For compound interest, N represents the number of compounding periods in the term. Thus, we need to calculate N before using the compound interest future value formula (Formula 2.4a). Also, for compound interest problems, we use the periodic interest rate per compounding period (asciimathi/asciimath).

Aimed at the FIRE movement, this calculator helps individuals determine how much they need to save to retire future value of annuity early. It considers current savings, desired retirement age, expected lifestyle expenses, and other financial variables. Determining whether annuities are a good investment hinges on various factors, including individual financial goals, risk tolerance, and the need for future cash flow stability. When comparing the future values of Ordinary Annuity and Annuity Due, the primary difference lies in the timing of payments and the subsequent impact on compounding. Annuity Due typically results in a higher future value compared to an Ordinary Annuity given the same terms, as each payment in Annuity Due benefits from an additional compounding period. An annuity’s present value is the value of its future payments to you in today’s dollars.